Calculadora de Taxas Equivalentes

Seja para calcular parcelas de dívidas ou de investimentos, a nossa calculadora de taxas equivalentes pode te ajudar! Entenda o que são taxas equivalentes, como calcular e veja como é fácil usar a nossa ferramenta.

O que são taxas equivalentes?

Você já ouviu falar em juros compostos? Eles também são conhecidos como “juros sobre juros” e estão presentes em empréstimos, financiamentos, cheque especial, investimentos da renda fixa e em muitos outros produtos financeiros.

Na prática, os juros compostos acrescentam sempre um valor a mais, definido por uma taxa em porcentagem, em uma quantia prévia, que aumenta período a período. Ao contrário dos juros simples, que incidem apenas sobre o capital inicial, os compostos sempre incidirão sobre o acumulado. Por isso, seu efeito é bem mais significante. Por exemplo:

Capital inicial: R$ 100

Taxa de juros mensal: 1%

No cálculo de juros compostos, a capitalização seria assim:

• mês 1: R$ 100 + 1% = R$ 101
• mês 2: R$ 101 + 1% = R$ 102,01
• mês 3: R$ 102,01 + 1% = R$ 103,03

Entendeu?

Imagine, então, que temos um investimento rendendo uma taxa anual de 10% e queremos saber quanto vamos ganhar por mês. Nesse caso, como se trata de juros compostos, não basta dividir por 12: é aí que entram as taxas equivalentes.

Como calcular taxas equivalentes?

Para saber quanto uma taxa de juros compostos anual representa mensalmente e vice-versa, precisamos fazer o cálculo das taxas equivalentes. Mas você não precisa ser um gênio da matemática e nem ter muita aptidão com os números, pois a fórmula é bastante simples:

Taxa equivalente = [(1+ taxa) elevado a: prazo que quero/prazo que tenho – 1] x 100

No caso do nosso investimento mencionado antes, nossa taxa é de 10% ao ano, então, o prazo que temos é de 12 meses e o que queremos é de 1 mês. Para o cálculo, vamos tirar a porcentagem da taxa, bastando dividir por 100: 10/100 = 0,1. Agora é só aplicar a fórmula:

Taxa equivalente = [(1 + 0,1)^ 1/12 – 1] x 100

Taxa equivalente = [(1,1)^ 0,0833 – 1] x 100

Taxa equivalente = [1,0079 – 1] x 100

Taxa equivalente = 0,0079 x 100

Taxa equivalente = 0,79% ao mês

Assim, sabemos que uma taxa anual de 10% equivale a uma taxa mensal de 0,79% (ou 0,8%, arredondando). Fácil, né?

Como calcular juros de 1% ao mês?

Para exemplificar, vamos imaginar a mesma ocasião para os dois tipo de juros (simples e compostos), onde você fez um empréstimo de R$ 1 mil. A taxa de juros é de 1%. E o tempo é 4 meses.

Juros simples

No caso dos juros simples, o valor aumentará em 1% (ou R$ 10) a cada mês, não importa o que aconteça. Ou seja:

1.000 x 0,01 = 10

Sendo assim, as parcelas serão uma parte dos R$ 1.000,00 que pegou de crédito + R$ 10,00 de juros.

Logo, supondo que o pagamento do valor inicial foi divido em 4 vezes. É preciso, dividir R$ 1.000,00 por 4 e adicionar a taxa de juros encontrada, no caso R$ 10,00. Veja:

Primeiro mês: 250 + 10 = R$ 260,00
Segundo mês: 250 + 10 = R$ 260,00
Terceiro mês: 250 + 10 = R$ 260,00
Quarto mês: 250 + 10 = R$ 260,00

Portando, a somatória ao final de 4 meses será de R$ 1.040.

Juros Compostos

Ao pensar nos juros compostos, o valor aumenta sempre de acordo com os juros do mês anterior. Ou seja, se no primeiro mês houve o mesmo aumento de 1% (ou R$ 10), no segundo mês este aumento será de R$ 10,10. Observe:

Primeiro mês:  1.000 x 0,01 = R$ 10,00
Parcela 1: 250 + 10 = R$ 260,00

Segundo mês: 1.010 x 0,01 = 10,10
Parcela 2: 250 + 10,10 = R$260,10

Terceiro mês: 1.020,10 x 0,01 = 10,20
Parcela 3: 250 + 10,20 = R$ 260,20

Quarto mês: 1.030,30 x 0,01 = 10,30
Parcela 4: 250 + 10,30= R$ 260,30

Total do valor pago com juros = R$ 1.040,60

Como usar a calculadora de taxas equivalentes?

Agora que você já sabe como calcular a taxa equivalente, saiba que não precisa ter esse trabalho toda vez: a nossa calculadora de taxas equivalentes já faz isso para você! Para usar, basta colocar a taxa que você tem e se ela é mensal ou anual e pronto! Seu resultado aparece logo abaixo.

Converter taxa anual para mensal

Para converter uma taxa anual de juros em uma taxa mensal utilizando a calculadora de taxas equivalentes do iDinheiro, basta inserir no campo “Taxa a ser Convertida” o valor referente a taxa que deseja saber.
Em seguida, no item “Tipo da Taxa de Entrada” selecione a opção “anual”. Depois preencha o tópico “Tipo da Taxa de Saída” com a alternativa “mensal”.

Pronto, agora é só clicar no botão “Calcular” que a ferramenta irá apresentar o resultado de acordo com a taxa aplicada, convertendo-a de anual em mensal.

Além de gerar o resultado, a ferramenta ainda disponibiliza algumas opções de corretoras para analisar, caso deseja investir.

Veja um exemplo:

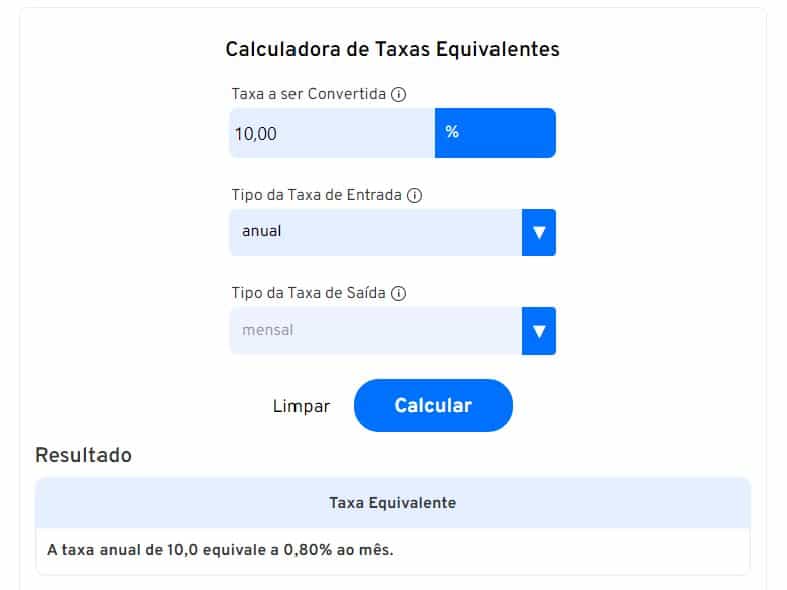
Converter taxa mensal para anual

No entanto, caso desejar converter uma taxa mensal de juros em uma taxa anual utilizando a calculadora de taxas equivalentes do iDinheiro, basta seguir a mesma etapa mencionada anteriormente, apenas inverta os campos. Ou seja, insira no campo “Taxa a ser Convertida” o valor referente a taxa mensal.

Em seguida, no item “Tipo da Taxa de Entrada” selecione a opção “mensal”. Depois preencha o tópico “Tipo da Taxa de Saída” com a alternativa “anual”.

Pronto, agora é só clicar no botão “Calcular” que a ferramenta irá apresentar o resultado de acordo com a taxa aplicada, convertendo-a de mensal em anual.

Por fim, caso queira converter uma nova taxa, clique no botão “limpar” que a ferramenta apagará os dados mencionados, a fim de realizar uma nova análise.

Use-a sempre que precisar fazer essa conversão de taxas, seja para calcular a parcela de uma dívida ou saber quanto seu investimento vai render no período.

Veja também: Calculadora de Juros Compostos: cálculo de juros sobre juros

Perguntas frequentes